Series and parallel resonance of crystal
The nominal operating frequency of a quartz crystal is usually marked on its outer casing, but this is just an approximate value. In reality, the crystal has multiple resonant frequencies, even under ideal conditions. This behavior arises from the internal structure of the crystal, which can be modeled as an equivalent electrical circuit.
Figure 1 shows the equivalent circuit of an ideal quartz crystal. It consists of three main components: a series combination of an inductor L1 and a capacitor C1, along with a parallel capacitor C2 connected across them. This configuration helps explain the two distinct resonant frequencies that the crystal exhibits.
At a specific **series resonant frequency**, the impedance (Z) of the circuit becomes zero. This happens when the inductor L1 and the capacitor C1 are in series resonance, effectively canceling each other out. At this point, the parallel capacitor C2 has no effect on the circuit's behavior.
However, at a different **parallel resonant frequency**, the input impedance reaches its maximum, theoretically approaching infinity. This occurs when the series combination of L1 and C1 resonates in parallel with C2. For this to happen, the parallel resonance must occur at a slightly higher frequency than the series resonance. As a result, the parallel resonant frequency is always greater than the series resonant frequency, even by a small margin.
The choice between using series or parallel resonance depends on the application. In some cases, the series resonance is more critical, while in others, the parallel resonance plays a more important role.
Mathematically, the impedance Z of the crystal can be expressed as:
$$
Z = \frac{1}{j\omega C_2 + j\omega C_1 + \frac{1}{j\omega L_1}}
$$
From this, we can derive the formulas for both resonant frequencies:
- **Series Resonant Frequency**:
$$
F_{\text{series}} = \frac{1}{2\pi \sqrt{L_1 C_1}}
$$
- **Parallel Resonant Frequency**:
$$
F_{\text{parallel}} = \frac{1}{2\pi \sqrt{\frac{L_1 C_1 C_2}{C_1 + C_2}}}
$$
As shown in Figure 3, the parallel resonant frequency is always higher than the series resonant frequency. This relationship is crucial for designing oscillator circuits and ensuring stable frequency operation in electronic devices. Understanding these resonant behaviors allows engineers to optimize the performance of quartz-based systems.
8KW-30KW MPPT Single-Phase Hybrid Inverter
8KW-30KW SIngle-Phase Hybrid Inverter(MPPT)
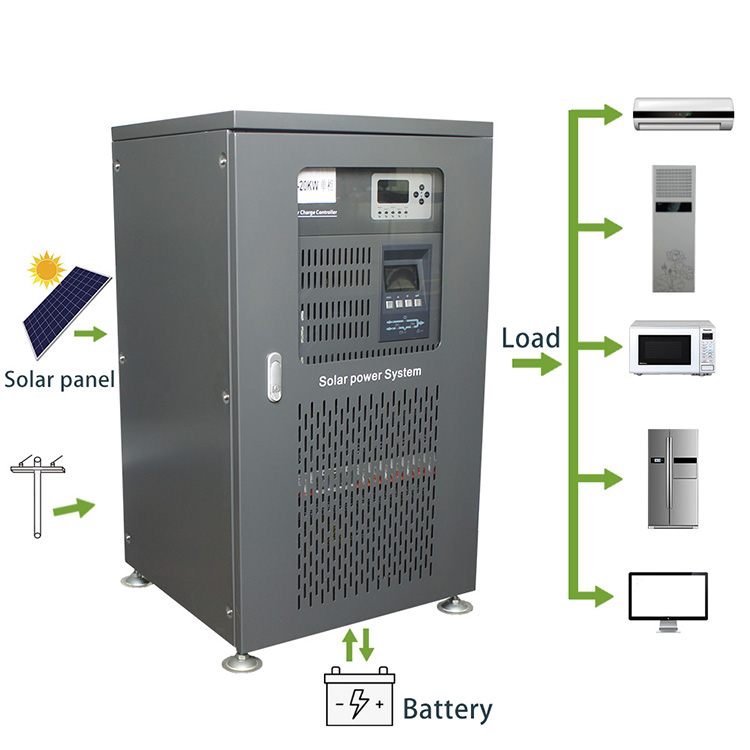

8KW-30KW MPPT Single-Phase Hybrid Inverter,Hybrid Solar Inverters, 48v Hybrid Solar Inverter
suzhou whaylan new energy technology co., ltd , https://www.xinlingvideo.com